The fundamental theorem of algebra tells us in short that complex numbers have complex roots with the number of roots being the highest degree in the polynomial. In class we talked about how it was a big deal and the two main reasons that made it such a big deal. The first reason was because it means that numbers are algebraically closed. While this happens it doesn’t mean that integers are closed, because they are not. When you write down a polynomial it is very rare that you will get integers as the solution. You may see this happen but most likely it will not. The second reason it is a big deal is because it means that every polynomial factors into quadratic and linear factors. This means that to understand all polynomials, we need to understand linear and quadratic equations. That should pretty much be second nature to us.
Gauss’ thesis has several proofs but later on they have found some problems in them. Later in his life, he was able to give a good enough proof that satisfied even a modern algebraist. There are not many purely algebraically pure proofs of the fundamental theorem of algebra but Gauss used one neat idea within his proof that we talked about in class. Gauss used Eulers identity to separate polynomials into a real and complex part. In order for Gauss to be able to do this he needed to turn complex numbers from his notation, which was a+bi into the notation re^(iθ). In this equation r is the magnitude and θ is the direction, I is an imaginary number, and e is Eulers number.
A specific example follows. We will turn the equation a+bi into re^(iθ) using actual number. This will allow us to be able to understand exactly what Gauss is doing and allow us to understand it to be able to use it in other examples. We will use the equation 2+2i which is in Gauss’ form and transport it into re^(iθ).
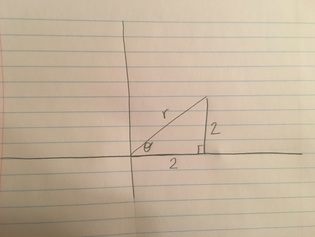
First we need to make a triangle on an axis using the equation 2+2i. We need to make this triangle a right triangle so we can use trig functions eventually, which is shown below. We will have the first 2 as the base and the second 2 as the opposite side from the angle of the triangle.
22+22=c2
8=c2
sqrt(8)=c
We know have found our hypotheses which is also our magnitude to be sqrt(8) so we have now found out r in the equation we are trying to find.
When going about this part I was really excited because I love algebra and the Pythagorean theorem is just that. When talking about making the triangle I had to remind myself what part of the equation would go where on the triangle but that didn't take long.
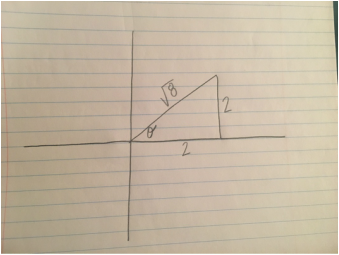
tan(x)=4/3
Since 4 is our opposite side of the angle and 3 is the adjacent side to the angle. When calculating this we use arctan(4/3) and we obtain π/4. So now we have found our direction which we know is θ in our equation. We now have all the parts we need to be able to put the equation together. Which we get to be sqrt(8)e^(i( π/4)). This is the equation that helped Gauss get through the proof of fundamental theorem of algebra. If you ever read this proof, when it comes to this part you should now be able to understand what is happening and why he does what he does.
While calculation this part it brought me back to when I was learning trigonometry. I will never forget s o/h c a/h t o/a and find it fun to work with. The only thing that was hard for me was when calculating arctan(4/3) making it into radiants of a fraction not just the decimal. I had to try to remember the unit circle we focused on so much in trigonometry. Finally I was able to figure it out. After I found that part the rest was just plug what we needed/found into our equation which is the easiest part.
Working through this part of his proof during class really allowed us to get a feel for things that gauss did and his thinking behind it. It allowed us to be able to see different aspects that go into the fundamental theorem of algebra and how seeing the work behind it better helps us understand it. I believe that this is important in a classroom. In order for kids to really understand what they are doing they need to work through what it is that they are doing and understand why they are doing it.
 RSS Feed
RSS Feed
